Team:Lethbridge Canada/math
From 2014hs.igem.org


Lethbridge High School

Project
Math
To find the amount of ampicillin inside of a system (relative to a starting concentration) we must be able to calculate how fast ampicillin is removed from the system. We used a closed environment (dialysis experiment) and placed ampicillin resistant bacteria into spiked media and took measures every hour of the ampicillin concentration (relative to the CFU assay) and plotted a graph of the ampicillin concentration versus time. This allows us to find how much ampicillin we will lose over a period of time. This assumes beta-lactamase to be a black box, but we would like to elucidate its role in the degradation of ampicillin, so we started by modeling the growth of beta-lactamase over time with the intent of finding the rate at which beta lactamase catalyses ampicillin.
AMPICILLIN
We currently have a graph of our colony forming units versus time spent in the dialysis experiment, but our baseline to compare # of colony forming units to concentration of ampicillin is skewed due to errors in experimentation. We will be able to provide a graph of ampicillin concentration vs. time at the jamboree, but for now we only have colony forming units vs. time.
Graph of CFU’s vs time From this, you can see that the amount of ampicillin decreases with increasing time. This is a result of more Beta-lactamase being produced by the cells, which degrades our antibiotic. In the future we would like to expand this to different values of E0 and plot concentration vs time instead of CFUs. With this information we could define a rate constant for the degradation of ampicillin relevant to initial volumes of ampicillin and e.coli by defining functions that relate [A] to time. We can see how these relate relative to E0 and form an equation looking something like this:
_.png)
BETA LACTAMASE
NUMBER OF E. COLI
To find the total amount of Beta-lactamase produced by each cell, the initial number of bacteria must be determined:
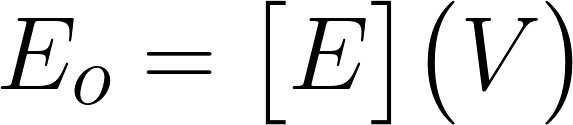
FORWARD (SYNTHESIS) RATE OF BETA LACTAMASE:
The following expression calculates the rate that Beta-lactamase is produced for a single cell by determining the product of the Amino Acids produced per second and the inverse of Amino Acids per Beta lactamase with the following expression: Credits go to the 2009 Beijing iGEM team for calculating the average translation speed of e. coli.

This determines the amount of Beta-lactamase produced per second by each individual bacteria.
TOTAL AMOUNT OF BETA LACTAMASE PRODUCED:
Now we have to factor in the amount of e.coli we have at any given point in time. Assuming we are in doubling phase the whole time, we can (very closely) approximate the doubling time of e.coli and solve for the number of e.coli in our system at any time, and therefore, the

REVERSE (DEGRADATION) RATE OF BETA LACTAMASE:
To determine the amount of Beta-lactamase that is being lost over time, two variables are used in the following expression:
_copy.png)
OVERALL BETA LACTAMASE PRESENT:
We combine both expressions for the Forward (synthesis) rate and the Reverse (degradation) rate for Beta-lactamase:
.png)
By including the half-life of Beta-lactamase we come across an implicit differential equation in the final expression and this practically unsolvable by hand. We tried using the mathematical software Maple to solve it; unfortunately we couldn’t make it work in the end and are left to make some approximations. We will assume that if we experiment for less than an hour we can ignore the half life of beta lactamase and get the following equation again.

However, if we have larger periods of time we cannot reliably calculate the amount of beta lactamase we have. In the future, we would like to reliably calculate the number of beta lactamase in the system at any point in time, and then calculate the rate at which beta lactamase will degrade ampicillin as a function of time, hopefully giving similar values to the ampicillin rate constant.

REFERENCES:
https://2009.igem.org/Team:PKU_Beijing/Modeling/Parameters
 "
"