Mathematical Model

Purpose

In order to obtain optimal results from each one of our experiments, the Montgomery iGEM team has undertaken the challenge of using differential calculus concepts to model the rates of growth of protein. First, we seek to model the theoretical amount of proteins expressed by the bacteria's gene. The quantity of protein yielded by the bacteria is especially important due to the exacting amount of protein necessary to effectively alter enough sebum molecules and cut off P. acnes's nutrient source. Because enzyme productivity is dependent on protein output, we will be able to model the enzyme kinetics, the rate at which conformations of sebum components are broken down.

Defining our Model

Assumptions

• We assume that bacteria follows logistical growth.
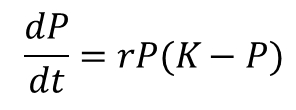
• The bacteria expresses the gene to produce the protein. In the actual experiment, we failed to effectively transform the bacteria. However, because this may be due to human error, we assume that the recombinant plasmid is effectively transformed into the bacteria. Thus the model demonstrates purely theoretical results based on optimal lab procedure.
• We assume that we are dealing with a single-step enzymatic reaction.

Parameters

• Doubling time of bacteria: 30 minutes
• The maximum rate at which DNA is transcribed in to mRNA in E.coli, as determined by the 2009 Beijing iGEM team is 4200nt/min.
• The average speed of translation in E. coli is 2400Aa/min, as calculated by the 2009 Beijing iGEM team.

The Math

The rate of transcription is constant and independent of the concentration of any species involved.

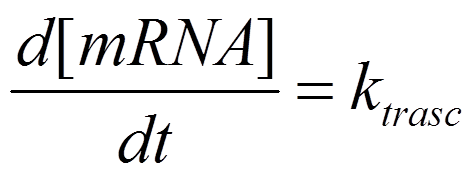
The rate of translation (from mRNA to protein) is dependent on the amount of mRNA. We must determine the rate constant, k, experimentally.

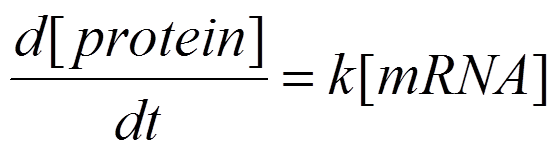
We must also take into account the degradation of mRNA and protein. The equations become:

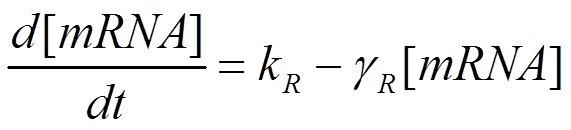
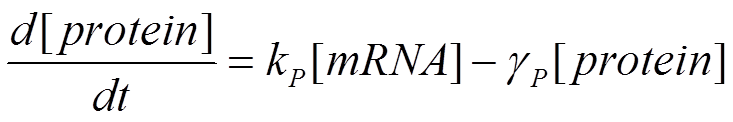
Enzyme Kinetics

Enzymes are proteins that catalyze chemical reactions. The typical enzyme (E) converts a substrate (S) into a product (P), as exemplified by the chemical formula:

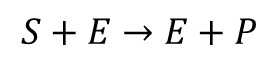
The rate at which the concentration of a product increases in proportion to the concentration of reactants. Thus:

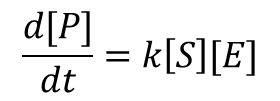
In which:

Enzyme (E): Dehydrogenase

Substrate (S): Lacl

Product (P): Altered wax ester.

By increasing the enzyme concentration (the dehydrogenase) while keeping the substrate concentration constant, we can increase the initial rate (v) at which the product is formed (which is the altered sebum components rendered unfit to be P. acnes's nutrient source). The optimal result from our bacterial transformation would be to create a machine that can express the creation of the enzyme that increases the rate until the addition of more substrate no longer has an effect and the enzyme is saturate with substrate.