Team:Jefferson VA SciCOS/Project
From 2014hs.igem.org
| (19 intermediate revisions not shown) | |||
| Line 2: | Line 2: | ||
{|align="justify" | {|align="justify" | ||
| | | | ||
| - | '''''Solving a 4-Node Traveling Salesman Problem Using the Hin/hixC Recombinant System''' | + | '''''<h3>Solving a 4-Node Traveling Salesman Problem Using the Hin/hixC Recombinant System</h3>''' |
---- | ---- | ||
| - | Our project’s goal was to assess the accuracy, scalability, and feasibility of a novel bacterial computer paradigm for solving a 4-node Traveling Salesman Problem. | + | Our project’s goal was to assess the '''accuracy''', '''scalability''', and '''feasibility''' of a novel bacterial computer paradigm for solving a 4-node Traveling Salesman Problem. |
|} | |} | ||
{|align="justify" | {|align="justify" | ||
| | | | ||
| - | '''''Bacterial Computing: The Future of the IT Industry All in an Agar Plate''' | + | '''''<h3>Bacterial Computing: The Future of the IT Industry All in an Agar Plate</h3>''' |
---- | ---- | ||
| - | Where would humanity be without the advent and rise of the computer? The 21st century has marked humanity’s entrance into a new Digital Age; now, more than ever, does the global marketplace and humanity itself depend on a thriving information technology sector. From the pocket-sized computing devices that we use to manage our day-to-day tasks to the massive supercomputers that mirror human intelligence, from the databases that store millions of patient’s records to the Big Data servers that analyze the vast number of financial transactions that take place every second, computing has evolved into a ubiquitous science that is both humanity’s present as well as its future. For years, the physical limitations that deterred the development of faster, more efficient computing devices were easily maneuverable, allowing computing to present itself as the seemingly perpetual gale force that propelled the sails of our global economy. | + | '''Where would humanity be without the advent and rise of the computer?''' The 21st century has marked humanity’s entrance into a new Digital Age; now, more than ever, does the global marketplace and humanity itself depend on a thriving information technology sector. From the pocket-sized computing devices that we use to manage our day-to-day tasks to the massive supercomputers that mirror human intelligence, from the databases that store millions of patient’s records to the Big Data servers that analyze the vast number of financial transactions that take place every second, computing has evolved into a ubiquitous science that is both humanity’s present as well as its future. For years, the physical limitations that deterred the development of faster, more efficient computing devices were easily maneuverable, allowing computing to present itself as the seemingly perpetual gale force that propelled the sails of our global economy. <br /> <br /> |
| - | But now, the winds of the Digital Revolution seem to be stilling. Little do people realize that Moore’s Law, the golden standard for advances in computing, is coming to an end. Moore’s Law, a bold vision for the future originally proposed in the early 1970s, set a clear goal for the future of computing hardware: every two years, the transistor count on a typical microprocessor (our computing capacity) would double. Now, however, we’ve finally hit the physical limit where transistors are packed so close together that reliable electron flow can no longer be sustained. This dilemma has raised a hue and cry throughout the computing industry, and has led to extensive research and development into new avenues of computing. Can we really transcend this computational limit? Could it be possible that the future of the computing industry be quantum computing? Or could it be something else? | + | '''But now, the winds of the Digital Revolution seem to be stilling.''' Little do people realize that Moore’s Law, the golden standard for advances in computing, is coming to an end. Moore’s Law, a bold vision for the future originally proposed in the early 1970s, set a clear goal for the future of computing hardware: every two years, the transistor count on a typical microprocessor (our computing capacity) would double. Now, however, we’ve finally hit the physical limit where transistors are packed so close together that reliable electron flow can no longer be sustained. This dilemma has raised a hue and cry throughout the computing industry, and has led to extensive research and development into new avenues of computing. Can we really transcend this computational limit? Could it be possible that the future of the computing industry be quantum computing? Or could it be something else? <br /> <br /> |
| - | Our group believes that synthetic biology, specifically the nascent field of bacterial computing, holds the key to the IT industry’s qualms. The computational capacity of biological systems is shockingly vast and amazingly robust. Unlike standard computers, bacterial computers may be able to autonomously solve quantitative problems in a massively parallel fashion; moreover, because bacteria are constantly dividing, the number of processors working on the problem grows exponentially with culture time. Also, bacterial computers use much less energy than standard computers to solve the HCP and the agar plates that they’re cultured on can even fit in the palm of your hand. | + | '''Our group believes that synthetic biology, specifically the nascent field of bacterial computing, holds the key to the IT industry’s qualms'''. The computational capacity of biological systems is shockingly vast and amazingly robust. Unlike standard computers, bacterial computers may be able to '''autonomously solve quantitative problems''' in a '''massively parallel''' fashion; moreover, because bacteria are constantly dividing, the number of processors working on the problem grows exponentially with culture time. Also, bacterial computers '''use much less energy''' than standard computers to solve the HCP and the agar plates that they’re cultured on can even '''fit in the palm of your hand.''' <br /> <br /> |
The 2007 Davidson-Missouri iGEM team demonstrated an algorithm using DNA constructs and the Hin recombinase/HixC site system capable of solving a three node Hamiltonian Path Problem. However, this team’s ground-breaking research left several questions unanswered that our group found critical to the future of bacterial computing: | The 2007 Davidson-Missouri iGEM team demonstrated an algorithm using DNA constructs and the Hin recombinase/HixC site system capable of solving a three node Hamiltonian Path Problem. However, this team’s ground-breaking research left several questions unanswered that our group found critical to the future of bacterial computing: | ||
| + | <ol> | ||
| + | <li>How accurate is bacterial computing? Can the algorithm be expected to reliably converge to a solution state regardless of the initial configuration? </li> | ||
| - | + | <li>How scalable is bacterial computing? Will our group be able to scale the technique up to larger node problems and how stable are hixC-site constructs for different proteins? Will our group be able to solve a completely different problem than the Hamiltonian Path Problem?</li> | |
| - | + | ||
| - | How scalable is bacterial computing? Will our group be able to scale the technique up to larger node problems and how stable are hixC-site constructs for different proteins? Will our group be able to solve a completely different problem than the Hamiltonian Path Problem? | + | |
| - | + | ||
| - | + | ||
| + | <li>How feasible is bacterial computing? Bacterial computing features a paradigm where the hardware is far cheaper than the software. How will this compare to other computing paradigms when we perform a cost-benefit analysis?</li> | ||
| + | </ol> | ||
With these guiding questions in mind, our group has proposed a project that assesses the accuracy, scalability, and feasibility of a bacterial computer paradigm for solving different initial configurations of a 4-node Traveling Salesman Problem. Our work proposes a novel way of encoding the Traveling Salesman Problem using variable Ribosome Binding Site strengths and DNA constructs that can be solved by the Hin recombinase/HixC site system. | With these guiding questions in mind, our group has proposed a project that assesses the accuracy, scalability, and feasibility of a bacterial computer paradigm for solving different initial configurations of a 4-node Traveling Salesman Problem. Our work proposes a novel way of encoding the Traveling Salesman Problem using variable Ribosome Binding Site strengths and DNA constructs that can be solved by the Hin recombinase/HixC site system. | ||
|} | |} | ||
| + | {|align="justify" | ||
| + | | | ||
| + | '''''<h3>The Traveling Salesman Problem</h3>''' | ||
| + | ---- | ||
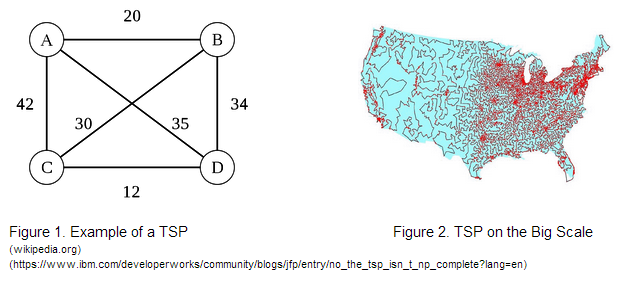
| + | Imagine you’re a salesman tasked with delivering goods to a set of towns. How can you find the shortest possible route to travel in order to visit every town exactly once to deliver your goods? This is exactly what the Traveling Salesman Problem seeks to find. The problem itself is extremely crucial to the transportation and shipping industry, where finding the shortest route possible can mean millions of dollars saved on the thousands upon thousands of goods delivered daily. Could bacteria performing computations in an agar plate hold the answer to this longstanding question? | ||
| + | [[File:Tsp.png]] | ||
| + | |} | ||
| + | {|align="justify" | ||
| + | | | ||
| + | '''''<h3>Taking a Previous Encoding Scheme a Step Further</h3>''' | ||
| + | ---- | ||
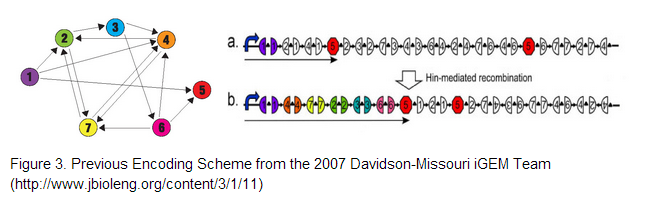
| + | The 2007 Davidson-Missouri iGEM team proposed three encoding schemes given by Figure 3, where cities correspond to given genes and adjacent gene halves separated by hixC sites represent edges on the graph. To encode our 4-node problem we decided on using genes encoding for (1). blue fluorescent protein , (2) green fluorescent protein , (3) red fluorescent protein and a (4) terminator. <br /> | ||
| + | [[File:Encoding.png]] | ||
| + | To encode for the distances between graphs we decided to use varying Ribosome Binding Strengths. Using the following gene sequence to RBS calculator (http://salis.psu.edu/RBS_Calculator.shtml), we proposed a function to go from the distance between cities to RBS. The function was constructed in such a way that the shorter the distance between cities, the greater the RBS. This way the solution encoding for a path with the shortest distance would fluoresce the brightest. | ||
| + | |} | ||
| + | {|align="justify" | ||
| + | | | ||
| + | '''''<h3>Engineering Our BFP Construct</h3>''' | ||
| + | ---- | ||
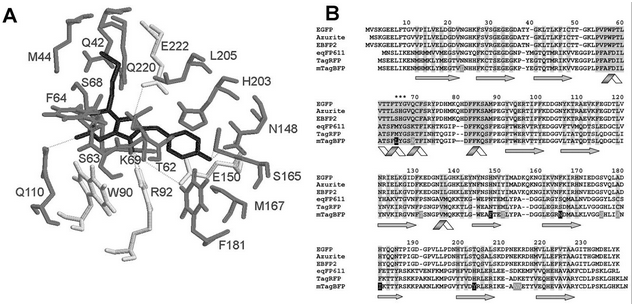
| + | In order to carry out the encoding scheme we developed above, it was necessary to develop our own BioBrick to represent the two gene halves encoding for BFP. It was important to make sure that the protein’s fluorescent activity would not be compromised once the hixC site was inserted, i. e. our insertion could not occur within the BFP’s chromophore sequence. To discover what the chromophore sequence was for BFP, we read the documentation for Part:BBa_K592100 (mTagBFP as shown in the figure) as described by Subach et al., 2005 (http://www.ncbi.nlm.nih.gov/pmc/articles/PMC2585067/). | ||
| + | [[File:chromophore_subach.png]] | ||
| + | Figure from Subach et al., 2005. Letters specifying chromophore sequence are in black | ||
| + | |||
| + | After having found the sequence for BFP and taking due note of which region encoded the chromophore, we then performed an analysis through the online gene splitting tool provided by the 2007 Davidson-Missouri Team (http://gcat.davidson.edu/iGEM07/genesplitter.html) in order to determine the correct primer to order. The following is a selection of the output from our analysis: <br /> | ||
| + | [[File:output.png]] | ||
| + | |||
| + | |} | ||
| + | {|align="justify" | ||
| + | | | ||
| + | '''''<h3>The Hin Recombinase/hixC Site System</h3>''' | ||
| + | ---- | ||
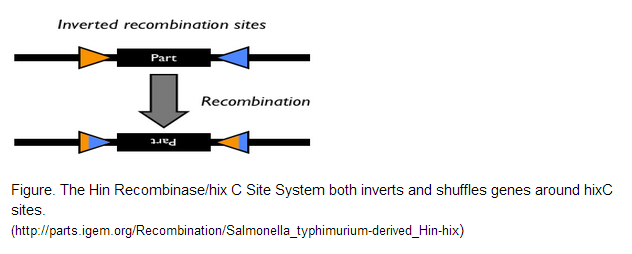
| + | The Hin Recombinase/hixC Site System is what breathes life into the encoding scheme we designed above. The system designed by a 2006 iGEM team is derived from Salmonella, where Hin regulates how flagellin genes are expressed. In our project, the system was used to constitutively shuffle the gene halves until a solution is arrived at. <br /> | ||
| + | [[File:Hin.png]] | ||
| + | |||
| + | |} | ||
| + | {|align="justify" | ||
| + | | | ||
| + | '''''<h3>The Path We Chose to Solve</h3>''' | ||
| + | ---- | ||
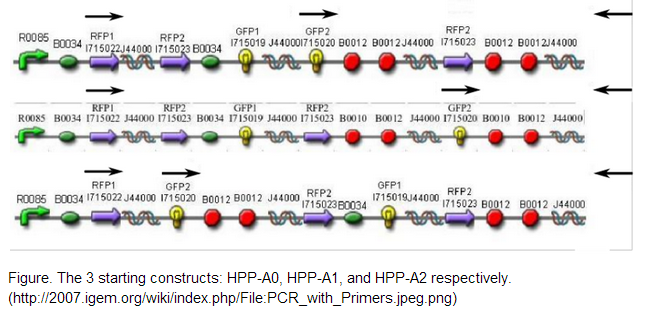
| + | The 2007 Davidson/Western Missouri iGEM team constructed 3 initial pathways to demonstrate that the Hamiltonian Path Problem could be solved in vivo. <br /> <br /> | ||
| + | [[File:Encoding2.png]] <br /> <br /> | ||
| + | We decided to use one of the starting constructs as a scaffold from which we could build our own composite pathway because each of the constructs contains three nodes: two split genes and a double terminator. Also, in the interest of time and resources, we were not concerned with constructing several pathways of our own as the Davidson/Western Missouri iGEM team had done. We ended up using HPP-A2 because it showed evidence of no fluorescence without Hin, which was the expected result as recorded by the Davidson/Western Missouri iGEM team. To HPP-A2, we added an RBS of moderate strength, as determined by the ribosome binding calculator and published values in literature. Compared to B0034, the RBS used in HPP-A2, B0032 is reported to exhibit 32% binding efficiency. Downstream of the RBS, we added another node: a BFP split-gene part. Thus, the order of our final part, from 5’ to 3’, was HPP-A2 + RBS + BFP1 + hixC + BFP2. We wanted to transform E.coli containing this composite pathway with Hin recombinase in order to shuffle the gene halves randomly and with varied efficiency, resulting in a solution to the TSP. | ||
| + | |} | ||
<html lang="en"> | <html lang="en"> | ||
<head> | <head> | ||
Latest revision as of 00:05, 21 June 2014
Solving a 4-Node Traveling Salesman Problem Using the Hin/hixC Recombinant SystemOur project’s goal was to assess the accuracy, scalability, and feasibility of a novel bacterial computer paradigm for solving a 4-node Traveling Salesman Problem. |
Bacterial Computing: The Future of the IT Industry All in an Agar PlateWhere would humanity be without the advent and rise of the computer? The 21st century has marked humanity’s entrance into a new Digital Age; now, more than ever, does the global marketplace and humanity itself depend on a thriving information technology sector. From the pocket-sized computing devices that we use to manage our day-to-day tasks to the massive supercomputers that mirror human intelligence, from the databases that store millions of patient’s records to the Big Data servers that analyze the vast number of financial transactions that take place every second, computing has evolved into a ubiquitous science that is both humanity’s present as well as its future. For years, the physical limitations that deterred the development of faster, more efficient computing devices were easily maneuverable, allowing computing to present itself as the seemingly perpetual gale force that propelled the sails of our global economy.
With these guiding questions in mind, our group has proposed a project that assesses the accuracy, scalability, and feasibility of a bacterial computer paradigm for solving different initial configurations of a 4-node Traveling Salesman Problem. Our work proposes a novel way of encoding the Traveling Salesman Problem using variable Ribosome Binding Site strengths and DNA constructs that can be solved by the Hin recombinase/HixC site system. |
 "
"